Pascal: программы, работающие в графическом режиме

Задача 1.

Построить семейство одинаковых окружностей, центры которых лежат на вертикально вращающемся отрезке, верхний конец которого закреплен.

Переменные:

x, y – координаты центра очередного маленького круга;
y0 – смещение кругов по вертикале;
i – переменная цикла;
t – угол поворота;
drive – тип графического драйвера;
mode – режим работы графического адаптера.

Для решения задачи:

инициируем модуль graph;
устанавливаем начальные значения радиуса, координаты центра;
организуем цикл, в котором закрашиваем круги со все большим радиусом до тех пор, пока не будет нажата любая клавиша.

uses crt,graph;
var drive,mode,x,y,i,t,y0:integer;
begin
   drive:=detect;
   initgraph(drive,mode,'c:\tp\bgi');
   setfillstyle(1,1);
   floodfill(1,4,1);
   t:=–4;
   y0:=10;
   setcolor(16);
   for i:=1 to 150 do
   begin
       t:=t+2;
       y0:=y0+3;
       x:=getmaxx div 2 + trunc(cos(t/10)*i);
       y:=y0 – trunc(sin(t/10)*i);
       setfillstyle(1,14);
       fillellipse(x,y,20,20);
       delay(100);
   end;
  repeat
  until keypressed;
  closegraph;
end.

uses crt,graph;

var drive,mode,x,y,i,t,y0:integer;

begin

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setfillstyle(1,1);

floodfill(1,4,1);

t:=–4;

y0:=10;

setcolor(16);

for i:=1 to 150 do

begin

t:=t+2;

y0:=y0+3;

x:=getmaxx div 2 + trunc(cos(t/10)*i);

y:=y0 – trunc(sin(t/10)*i);

setfillstyle(1,14);

fillellipse(x,y,20,20);

delay(100);

end;

repeat

until keypressed;

closegraph;

end.

Задача 2.

Построить движущиеся изображения НЛО на фоне звездного неба.

Переменные:

x, y – случайные координаты;
r – радиус;
i – переменная цикла;
drive – тип графического драйвера;
mode – режим работы графического адаптера.

Алгоритм решения задачи:

инициируем модуль graph;
организуем безусловный цикл по переменной i и рисуем звездное небо;
организуем цикл до тех пор, пока не будет нажата любая клавиша;
в этом цикле рисуем НЛО с помощью двух эллипсов, двух линий и двух маленьких кружочков, держим на экране, затем стираем изображение процедурой CLEARDEVICE;
опять рисуем звездное небо;
определяем случайным образом координаты следующего изображения НЛО;
после нажатия любой клавиши закрываем графический режим.

uses crt,graph;
var drive,mode,x,y,i,r:integer;
begin
   r:=40;
   x:=r*5;
   y:=r*2;
   drive:=detect;
   initgraph(drive,mode,'c:\tp\bgi');
   setcolor(3);
   for i:=1 to 600 do
      putpixel(random(i),random(i),i);
   repeat
       ellipse(x,y,0,360,r,(r div 3)+2);
       ellipse(x,y–4,190,357,r,r div 3);
       line(x–17,y–16,x–25,y–22);
       line(x+17,y–16,x+25,y–22);
       circle(x+25, y–25,2);
       circle(x–25, y–25,2);
       setfillstyle(1,3);
       floodfill(x+1,y+4,3);
       delay(150);
       cleardevice;
       for i:=1 to 600 do
           putpixel(random(i),random(i),i);
       x:=x+random(10);
       y:=y+random(10);
   until (keypressed);
  closegraph;
end.

uses crt,graph;

var drive,mode,x,y,i,r:integer;

begin

r:=40;

x:=r*5;

y:=r*2;

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setcolor(3);

for i:=1 to 600 do

putpixel(random(i),random(i),i);

repeat

ellipse(x,y,0,360,r,(r div 3)+2);

ellipse(x,y–4,190,357,r,r div 3);

line(x–17,y–16,x–25,y–22);

line(x+17,y–16,x+25,y–22);

circle(x+25, y–25,2);

circle(x–25, y–25,2);

setfillstyle(1,3);

floodfill(x+1,y+4,3);

delay(150);

cleardevice;

for i:=1 to 600 do

putpixel(random(i),random(i),i);

x:=x+random(10);

y:=y+random(10);

until (keypressed);

closegraph;

end.

Та же программа может быть написана с использованием пары процедур

    GETIMAGE(lx,ly,rx,ry,saucer^) и PUTIMAGE(x,y,saucer^,xorput).

1	GETIMAGE(lx,ly,rx,ry,saucer^) и PUTIMAGE(x,y,saucer^,xorput).

Процедура GETIMAGE(lx,ly,rx,ry,saucer^) помещает изображение в буфер, а PUTIMAGE(x,y,saucer^,xorput) выводит в заданное место изображение.
Параметр xorput определяет способ вывода на экран – исключающее ИЛИ.
Например, операторами

GETIMAGE(lx,ly,rx,ry,saucer^);
READLN;
PUTIMAGE(x,y,saucer^,xorput);

мы выводим изображение на экран и после нажатия любой клавиши стираем его.
Можно использовать другие способы вывода изображения на экран, например:

NORMALPUT – стирает часть экрана и на это место выводит изображение;
NOTPUT – делает то же самое, но изображение инвертируется;
ORPUY – дописывает новое изображение.

Переменные:

x, y – случайные координаты;
r – радиус;
i – переменная цикла;
saucer – указатель буфера хранения изображения;
drive – тип графического драйвера;
mode – режим работы графического адаптера.

Алгоритм решения задачи:

инициируем модуль graph;
рисуем НЛО с помощью двух эллипсов, двух линий и двух маленьких кружочков, держим на экране, затем стираем изображение процедурой CLEARDEVICE;
определяем размер буфера и помещаем в него изображение;
организуем безусловный цикл по переменной i и рисуем звездное небо;
организуем цикл до тех пор, пока не будет нажата любая клавиша;
опять рисуем звездное небо;
в этом цикле помещаем изображение из буфера на экран, держим его на экране, затем стираем изображение;
определяем случайным образом координаты следующего изображения НЛО;
после нажатия любой клавиши закрываем графический режим.

uses crt,graph;
var drive,mode,x,y,i,r,rx,ry,lx,ly,size:integer;
     saucer:pointer;
begin
   r:=20;
   x:=r*5;
   y:=r*2;
   drive:=detect;
   initgraph(drive,mode,'c:\tp\bgi');
   setcolor(3);
   ellipse(x,y,0,360,r,(r div 3)+2);
   ellipse(x,y–4,190,357,r,r div 3);
   line(x–17,y–16,x–25,y–22);
   line(x+17,y–16,x+25,y–22);
   circle(x+25, y–25,2);
   circle(x–25, y–25,2);
   setfillstyle(1,3);
   floodfill(x+1,y+4,3);
   lx:=x–r–30;
   ly:=y–30;
   rx:=x+r+30;
   ry:=y+r div 3+30;
   size:=imagesize(lx,ly,rx,ry);
   getmem(saucer,size);
   getimage(lx,ly,rx,ry,saucer^);
   readln;
   putimage(lx,ly,saucer^,xorput);
   for i:=1 to 600 do
       putpixel(random(i),random(i),i);
   repeat
       putimage(x,y,saucer^,xorput);
       delay(150);
       putimage(x,y,saucer^,xorput);
       x:=x+random(10);
       y:=y+random(10);
   until (keypressed);
   readln;
  closegraph;
end.

uses crt,graph;

var drive,mode,x,y,i,r,rx,ry,lx,ly,size:integer;

saucer:pointer;

begin

r:=20;

x:=r*5;

y:=r*2;

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setcolor(3);

ellipse(x,y,0,360,r,(r div 3)+2);

ellipse(x,y–4,190,357,r,r div 3);

line(x–17,y–16,x–25,y–22);

line(x+17,y–16,x+25,y–22);

circle(x+25, y–25,2);

circle(x–25, y–25,2);

setfillstyle(1,3);

floodfill(x+1,y+4,3);

lx:=x–r–30;

ly:=y–30;

rx:=x+r+30;

ry:=y+r div 3+30;

size:=imagesize(lx,ly,rx,ry);

getmem(saucer,size);

getimage(lx,ly,rx,ry,saucer^);

readln;

putimage(lx,ly,saucer^,xorput);

for i:=1 to 600 do

putpixel(random(i),random(i),i);

repeat

putimage(x,y,saucer^,xorput);

delay(150);

putimage(x,y,saucer^,xorput);

x:=x+random(10);

y:=y+random(10);

until (keypressed);

readln;

closegraph;

end.

Задача 3.

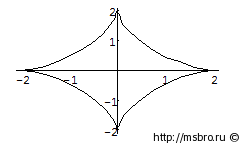
Построить астроиду-кривую, заданную параметрическим уравнением x = b cos3(t), y = b sin3(t), t принадлежит интервалу [0, 2(пи)]

Рис. 1 – Астроида

uses crt,graph;
const B=200;
var drive,mode,i:integer;
    x,y,t:real;
begin
   drive:=detect;
   initgraph(drive,mode,'c:\tp\bgi');     {инициализация графического режима}
   setcolor(3);
   line(10,240,630,240);                              {ось X}
   line(320,10,320,470);                              {ось Y}
   line(630,240,610,235);                            {стрелки на оси X}
   line(630,240,610,245);
   line(320,10,315,30);                                {стрелки на оси Y}
   line(320,10,325,30);
   t:=0;
   while t&lt;=2*pi do
   begin
         x:=b*sqr(cos(t))*cos(t);  {рассчитываем по формуле координаты то-чек}
         y:=b*sqr(sin(t))*sin(t);
         x:=320+x; y:=240+y;                         {рисуем в центре экрана}
        {рисуем точку с координатами x, y}
         putpixel(round(x),round(y),random(15)); t:=t+0.001;
  end;
  repeat until keypressed;
  closegraph;
end.

uses crt,graph;

const B=200;

var drive,mode,i:integer;

x,y,t:real;

begin

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi'); {инициализация графического режима}

setcolor(3);

line(10,240,630,240); {ось X}

line(320,10,320,470); {ось Y}

line(630,240,610,235); {стрелки на оси X}

line(630,240,610,245);

line(320,10,315,30); {стрелки на оси Y}

line(320,10,325,30);

t:=0;

while t<=2*pi do

begin

x:=b*sqr(cos(t))*cos(t); {рассчитываем по формуле координаты то-чек}

y:=b*sqr(sin(t))*sin(t);

x:=320+x; y:=240+y; {рисуем в центре экрана}

{рисуем точку с координатами x, y}

putpixel(round(x),round(y),random(15)); t:=t+0.001;

end;

repeat until keypressed;

closegraph;

end.

Oh, MSBRO !

Сетевые заметки системного администратора

Pascal: программы, работающие в графическом режиме